Упродовж останніх десяти років у США триває масштабна рецесія. Зважаючи на попередні бізнес-цикли, можна було б сподіватися на досить швидке повернення фактичного обсягу виробництва до його потенційного рівня – але не цього разу. Рис. 1 показує, що після великого спаду в 2008-2009 роках у США не спостерігається швидкого відновлення. Навпаки, темпи зростання сьогодні нижчі, ніж були до спаду.
Через це часто звучать запитання про те, чому сьогодні існує довгострокова стагнація, звідки вона взялася і що з цим усім робити?
Рис. 1. ВВП США, нормалізований так, що в першому кварталі 2007 року він дорівнює нулю
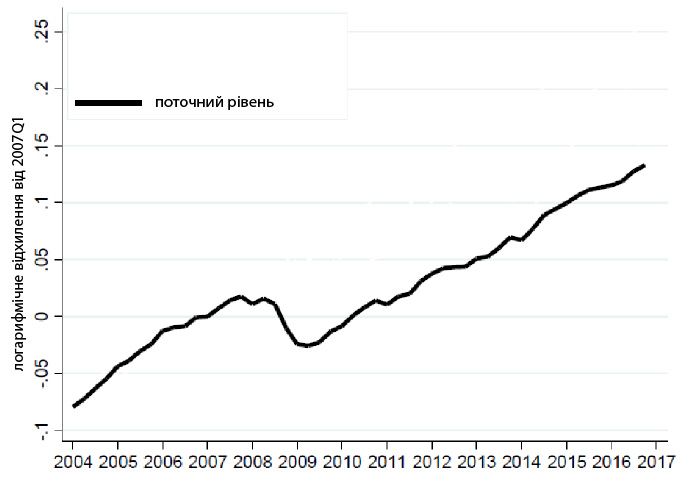
Рис. 2 показує фактичний ВВП (чорна лінія) порівняно з динамікою потенційного обсягу виробництва, яку розрахувало у 2007 Бюджетне управління Конгресу[1] (червона лінія). Цю ліню потенційного обсягу виробництва розрахували безпосередньо перед Великою рецесією з метою показати, що станеться у найближчі 10-15 років. В умовах типової рецесії ми побачили б, що чорна лінія поступово наближається до червоної лінії, але наразі ми не бачимо цього у фактичних даних. Ми бачимо натомість, як оцінений потенційний обсяг виробництва поступово наближається до фактичного обсягу (рис. 3).
Рис. 2. Динаміка фактичного обсягу ВВП порівняно з оціненим потенційним обсягом виробництва, за даними бюджетного управління Конгресу (БУК), 2007
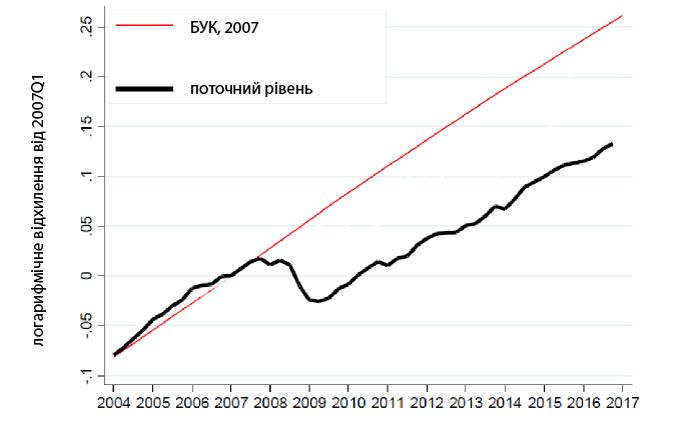
Рис. 3. Динаміка фактичного обсягу виробництва і перегляд оцінок БУК потенційного обсягу виробництва у вказані роки
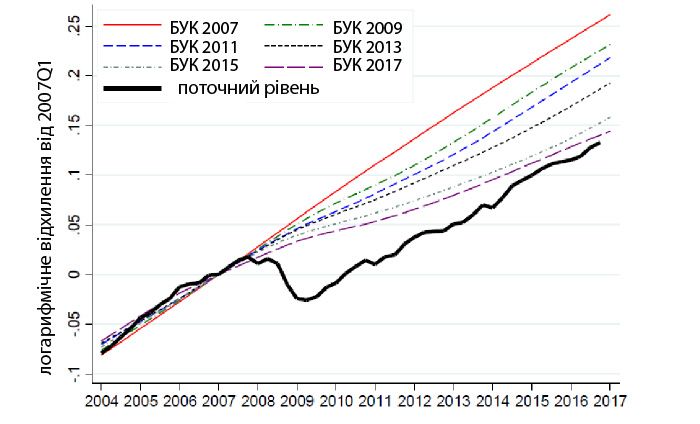
Сьогодні, як бачимо з рис. 3, потенційний обсяг виробництва дуже близький до фактичного, але близький не тому, що зріс фактичний обсяг, а через те, що показники оціненого потенційного обсягу виробництва були переглянуті у бік зниження.
Схоже, що дедалі більше людей вважає, що ми перебуваємо у стані дуже повільного зростання виробництва протягом тривалого часу.
Що це означає для центральних банків?
Чимало центральних банків сьогодні використовують правило Тейлора (1) або його модифікацію для визначення облікових ставок.
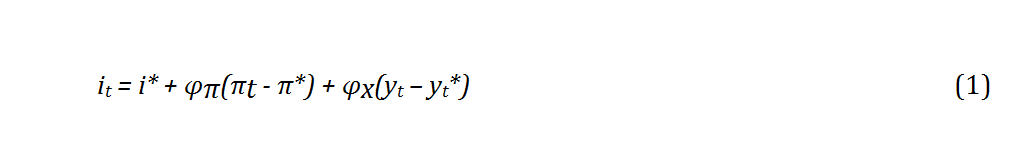
де it – облікова ставка центрального банку, i* – природний рівень відсоткової ставки (за умов повної зайнятості), πt і π* – поточний й очікуваний рівень інфляції, yt і yt* – зростання фактичного і потенційного ВВП, а φπ і φx – параметри економічної політики.
Розрив між фактичним і потенційним обсягом виробництва є одним із ключових параметрів цього правила (другий ключовий чинник – інфляційні очікування). Тому оцінка потенційного обсягу виробництва дуже важлива для центральних банків: якщо фактичний ВВП набагато нижчий за потенційний, центральний банк знизить свою облікову ставку або утримуватиме її на низькому рівні; якщо ж обсяг виробництва близький до потенційного або перевищує його, центральний банк може підвищити свою облікову ставку.
Отож, найголовніші питання, які стоять перед розробниками політики, звучать так:
Скільки невикористаного потенціалу ми маємо в економіці? і
Наскільки тривалими є відхилення від тенденцій, що існували до кризи?
Щоб відповісти на ці запитання, треба з’ясувати, що нам відомо про оцінений потенційний обсяг виробництва. І, зокрема, відповісти на запитання про те, навіщо взагалі переглядають оцінки потенційного обсягу виробництва.
На жаль, мало що відомо про те, як оцінюють потенційний обсяг виробництва і чому ці оцінки переглядають. Тому ця стаття має на меті розробити дуже просту статистичну схему, щоб зрозуміти основні властивості потенційного обсягу виробництва. Це може допомогти нам з’ясувати наслідки цього процесу для монетарної політики: як змінюється відстань між yt і yt* у правилі Тейлора у відповідь на різкі зміни в економіці (шоки)?
Для цього ми спершу зібрали показники потенційного обсягу виробництва у США та інших країнах, а потім проаналізували, як певні шоки впливають на фактичний обсяг виробництва й на поточні оцінки потенційного обсягу виробництва.
Ми дійшли таких висновків:
- Оцінки потенційного обсягу виробництва реагують на шоки і попиту, і пропозиції (тоді як теоретично потенційний обсяг виробництва має реагувати тільки шоки и пропозиції, а не шоки з боку попиту, які є тимчасовими)
- оцінки потенційного обсягу виробництва рано чи пізно збігаються з фактичним ВВП
- Властивості оцінок потенційного обсягу виробництва можна приблизно виразити за допомогою фільтру Ходріка-Прескотта. І це, мабуть, найбільш приголомшливий висновок нашого дослідження: усі надскладні моделі, які оцінюють потенційний обсяг виробництва, можна добре апроксимувати дуже простою статистичною схемою.
Отже, зниження потенційного обсягу виробництва не обов’язково є таким тривалим, як думають багато науковців і політиків. Можливо, ми просто спостерігаємо за негативним шоком, що триває довший час – і не більше.
Оцінки потенційного обсягу виробництва
Існує три основні підходи до оцінювання потенційного обсягу виробництва:
- За виробничою функцією.
Y* = f(K*, L*, продуктивність).
- Статистичний підхід.
Цей підхід передбачає використання різних методів для «очищення» даних від тимчасових шоків і коливань. Довгостроковий тренд, що залишається після цього, і є потенційним ВВП.
- Структурний підхід (найскладніший).
Згідно з цим підходом оцінюють структурну модель економіки (наприклад, динамічну модель загальної рівноваги), і в цій моделі потенційний обсяг виробництва є обсягом, який отримують, «виключивши» всі тимчасові шоки та чинники, що спричиняють неефективність.
Джерела даних
Існує кілька джерел оцінок потенційного обсягу виробництва:
- Бюджетне управління Конгресу (БУК), яке є «золотим стандартом» США для таких оцінок. Управління використовує підхід виробничої функції, а його дані покривають період від 1991 року до сьогодні
- Оцінки Ради Федеральної резервної системи («Зелена книга»), які використовуються для визначення монетарної політики. Вони вдаються до різноманітних методів, зокрема суб’єктивного, коли кілька експертів аналізують дані й використовують інформацію, яка не завжди входить до моделей, щоб упевнитися, що оцінка буде найкращою з можливих. Дані покривають період 1987-2011 рр. (Рада оприлюднює інформацію з п’ятирічною затримкою)
- МВФ, який також використовує комбінацію різних методів, зокрема суб’єктивний. Головною перевагою цього джерела є те, що МВФ має оцінки для багатьох країн, тобто можна використовувати не тільки варіацію часових рядів, а й варіацію оцінок потенційного обсягу виробництва за країнами.
- ОЕСР також використовує метод виробничої функції і надає дані щодо багатьох країн упродовж тривалого періоду.
- Оцінки приватного сектору (приватні прогнозисти не дають оцінок потенційного ВВП, тому ми використовуємо їхній довгостроковий – тривалістю до 10 років – прогноз фактичного ВВП)
Умовні факти
Перш ніж перейти до подальшого аналізу, ми хочемо представити кілька стилізованих фактів щодо оцінок потенційного ВВП.
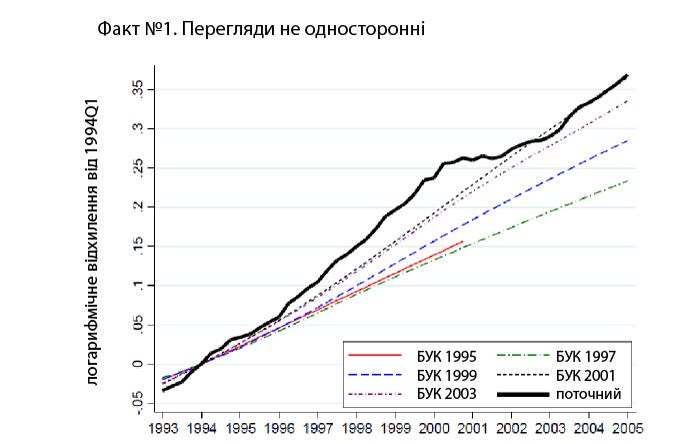
По-перше, потенційний ВВП може переглядатися як у бік зменшення, так і в бік збільшення. Прикладом перегляду вбік збільшення є друга половина 1990-х років, коли економіка США дуже швидко зростала (рис. 4).
Рис. 4. Перегляди потенційного ВВП у 1993-2005 рр.
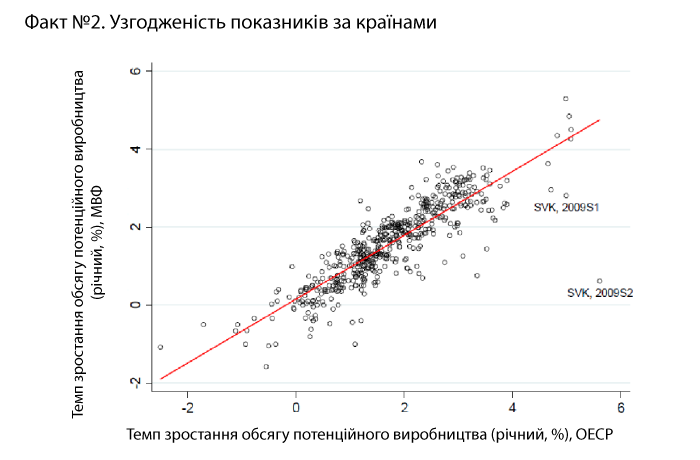
Другий факт полягає в тому, що різні джерела дають доволі узгоджені оцінки потенційного обсягу виробництва. Рисунок 5 демонструє, що кореляція між показниками потенційного обсягу виробництва, розрахованими ОЕСР, і тими, що їх розрахував МВФ, дуже тісна – близько 0,99. Очевидно, різні установи розраховують потенційний обсяг виробництва у приблизно однаковий спосіб.
Рис. 5. Кореляція між оцінками МВФ і ОЕСР щодо зміни потенційного ВВП
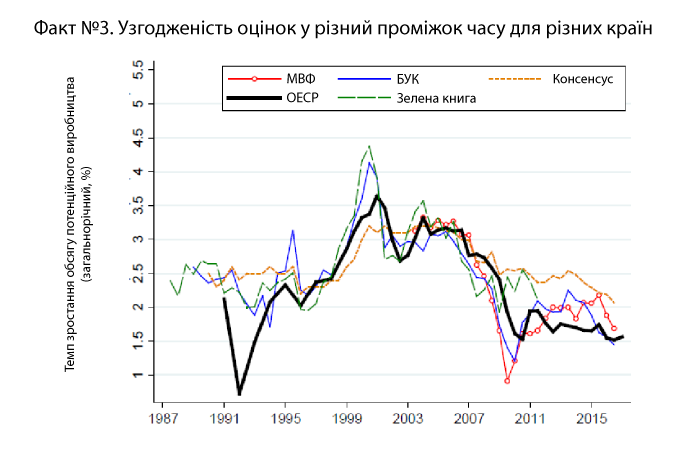
Оцінки різних установи узгоджуються між собою не тільки за країнами, а й у часі (рис. 6). На рис. 6 також показано, що з плином часу оцінки потенційного обсягу виробництва суттєво коливаються.
Рис. 6. Оцінки потенційного обсягу виробництва від різних установ у різний проміжок часу та в різних країнах
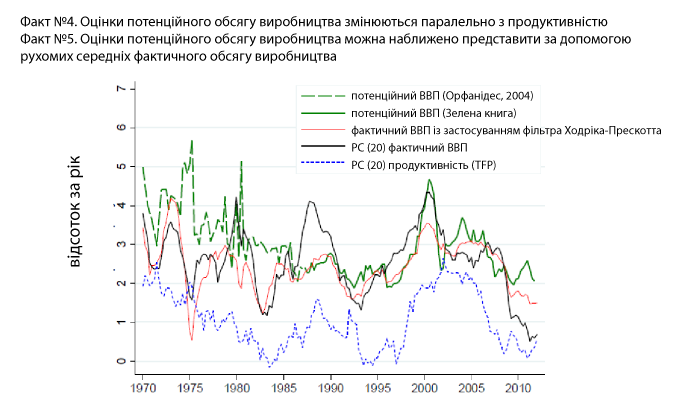
На рис. 7 показано ще два стилізовані факти: (1) оцінки потенційного обсягу виробництва суттєво корелюють зі змінами продуктивності (зелена і синя лінії на рис. 7) та (2) оцінки потенційного обсягу виробництва можна дуже добре апроксимувати ковзаючим середнім фактичного обсягу виробництва (червона й чорна лінії).
Рис. 7. Порівняння оцінок потенційного обсягу виробництва зі зростанням продуктивності і згладженим фактичним обсягом виробництва
Тепер перевіримо, як оцінки потенційного обсягу виробництва реагують на різні типи шоків. З цією метою оцінимо регресії методом найменших квадратів (OLS) із залежною змінною “зміни потенційного обсягу виробництва” та отримаємо для них функції реакції на імпульс (impulse response functions).
Теоретично потенційний обсяг виробництва має реагувати на довготривалі шоки з боку пропозиції. Прикладами таких шоків є: (1) підвищення продуктивності – наприклад, удосконалення технології; (2) постійна зміна режиму оподаткування – до прикладу, якщо податок на доходи фізосіб скорочують, люди починають працювати більше; (3) різка зміна ціни на нафту – еластичність попиту на енергоносії низька, тому зміна ціни на нафту впливає на продуктивність.
І навпаки: різкі зміни з боку попиту, які є причиною бізнес-циклів, є тимчасовими, а, отже, не мають впливати на оцінки потенційного обсягу виробництва. Прикладами шоків з боку попиту є (1) різкі зміни монетарної політики, як-от зміна облікової ставки центрального банку; (2) зміна державних видатків (наприклад, збільшення витрат на армію).
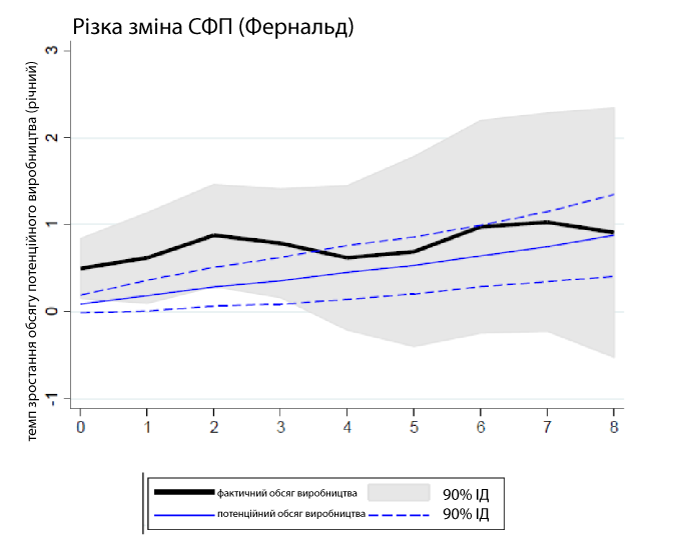
На рис. 8 показана реакція фактичного (чорна лінія) і потенційного обсягу виробництва (синя лінія) на різкі зміни продуктивності. Ми бачимо, що фактичний ВВП зростає відразу після шоку, а тоді залишається на новому, вищому, рівні. Таку ж динаміку мав би проявити й потенційний обсяг виробництва. Натомість спостерігаємо поступове збільшення потенційного обсягу виробництва, аж поки різниця між фактичним і потенційним ВВП не зникне. Подібну картину спостерігамо й з іншими шоками з боку пропозиції.
Рис. 8. Функція реакції на імпульс (постійний шок з боку пропозиції – зростання продуктивності)
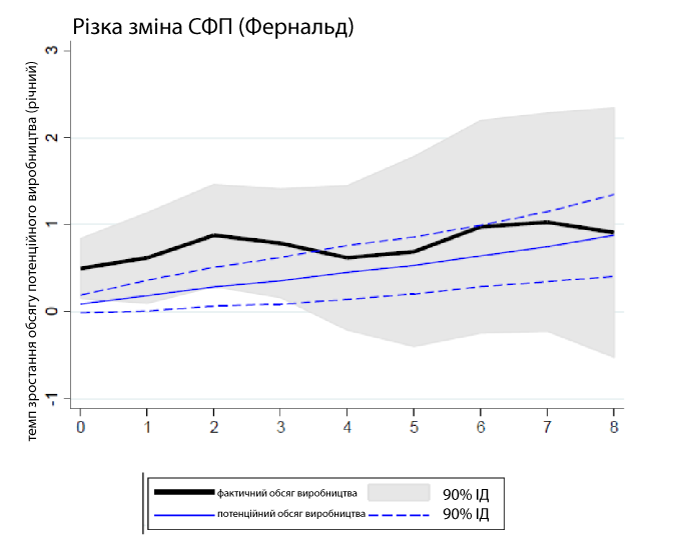
Розглянемо приклад шоку з боку попиту (рис. 9) – непередбачене скорочення державних видатків. Спочатку фактичний обсяг виробництва знижується, але потім швидко повертається до довгострокової тенденції. Потенційний обсяг виробництва спершу не реагує на зміну, але потім починає збільшуватися, що насправді нелогічно. Потенційний обсяг виробництва не має реагувати на тимчасові різкі зміни попиту.
Рис. 9. Функція реакції на імпульс (шок з боку попиту – скорочення державних видатків)
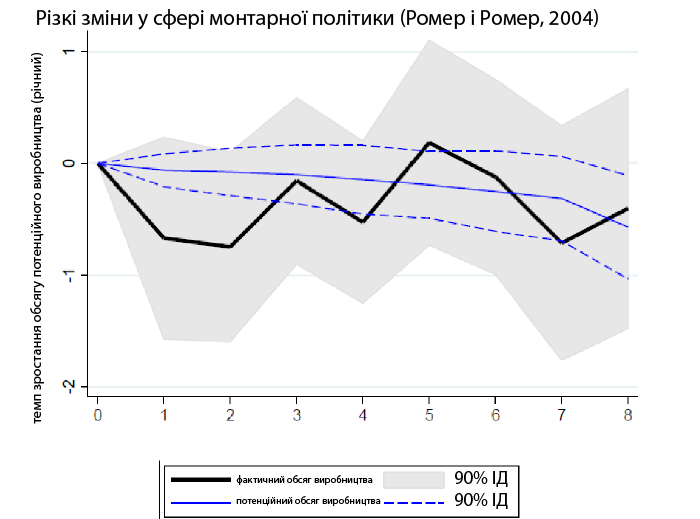
Ще один добрий приклад – різка зміна монтарної політики (мал. 10). Коли монетарна політика стає більш жорсткою, фактичний обсяг виробництва спочатку не реагує, а потім дещо скорочується. Дивно, що потенційний обсяг виробництва також суттєво реагує на шок монетарної політики, тоді як не мав би цього робити, адже, як відомо, такі шоки тимчасові й не впливають на виробничі потужності економіки.
Рис. 10. Функції реакції на імпульс фактичного й потенційного ВВП (шок з боку попиту – зміна монетарної політики, наприклад, підвищення відсоткової ставки)
Отримавши ці несподівані результати, ми вирішили дослідити, чому потенційний обсяг виробництва реагує – хоча й повільно, але сильно – на всі шоки. Для цього ми повторили всі попередні оцінки, але взявши як залежну змінну фактичний обсяг виробництва, “згладжений” за допомогою фільтра Ходріка-Прескотта. Ми помітили, що функції реакції на імпульс цієї змінної на шоки попиту та пропозиції статистично не відрізняються від функцій реакції на імпульс потенційного обсягу виробництва (на рис. 11 червона лінія розташована дуже близько до синьої лінії).
Рис. 11. Функції реакції на імпульс для фактичного обсягу виробництва, потенційного обсягу виробництва і фактичного обсягу виробництва, “згладженого” із застосуванням фільтра Ходріка-Прескотта
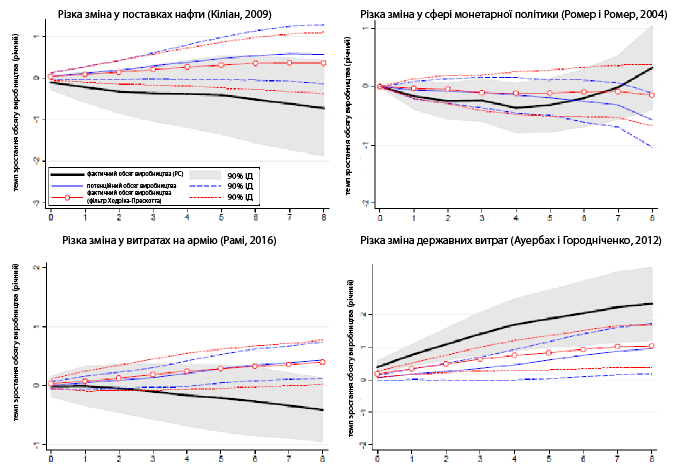
Ми провели той самий експеримент із даними з різних країн і отримали дуже схожі результати.
Висновки
Як приватні, так і державні оцінки потенційного ВВП поступово, але систематично реагують на всі економічні шоки, які ми розглядаємо, і їхня реакція практично не відрізняється від тієї, яку можна було б очікувати від простих авторегресійніх оцінок потенційного ВВП.
Те, що приватні та державні прогнозисти пояснюють зниження обсягу виробництва в різних країнах після Великої рецесії змінами потенційного ВВП, мало каже нам про те, чи ці зміни обсягів виробництва триватимуть довший час, чи ситуацію можна розвернути за допомогою монетарної чи фіскальної політики.
Отже, є потреба у використання додаткових макроекономічних змінних для кращої ідентифікації шоків попиту та пропозиції, аніж просто використання одновимірних прогнозів. Також варто поєднувати інформацію із державних оцінок потенційного ВВП з прогнозами приватного сектору, оскільки приватний сектор, схоже, ліпше вміє відрізняти шоки пропозиції від змін попиту. Оцінюючи потенційний ВВП, треба уникати надмірного згладжування за допомогою моделей, оскільки це автоматично призводить до змін в оцінках потенційного ВВП внаслідок циклічних коливань, викликаних попитом.
Загалом, відсутність чітких способів успішного оцінювання потенційного ВВП наштовхує на думку про те, що практика покладатися на «судження» професійних економістів найближчим часом не зникне.
Запитання: На мою думку, одним із висновків вашого дослідження є те, що уряд США й уряди інших держав мають продовжувати експансіоністську монетарну й фіскальну політику, оскільки, згідно з розрахунками БУК, нинішній фактичний обсяг виробництва навряд чи близький до потенційного. Відмова від експансіоністської політики, скоріше за все, призведе до затягування стагнації.
Відповідь: Так, наше дослідження може свідчити про те, що висновки про сьогоднішнє наближення економіки до стану повної зайнятості можуть бути суто статистичним аретфактом. Деякі ознаки свідчать, що економіка США наразі далека від стану повної зайнятості – наприклад, кількість працевлаштованих людей відносно загальної кількості населення досі не повернулася на докризовий рівень. Проте існує низка альтернативних інтерпретацій, які також узгоджуються з нашими результатами. Приголомшує те, що ми часто буквально обчислюємо різницю між фактичним і потенційним обсягом виробництва й будуємо навколо цього політику. Наша праця показує, що поняття, яке ми називаємо потенційним обсягом виробництва, потребує дуже уважного тлумачення, бо це не обов’язково справжній потенційний ВВП.
Примітки:
[1] незалежна інституція, що забезпечує найбільш повний та глибокий аналіз усіх питань, пов’язаних з бюджетом США, в тому числі надає макроекономічний прогноз – прим.ред.
Головне фото: depositphotos.com / tycoon
Застереження
Автори не є співробітниками, не консультують, не володіють акціями та не отримують фінансування від жодної компанії чи організації, яка б мала користь від цієї статті, а також жодним чином з ними не пов’язаний