У статті стисло розглядається Закон Бенфорда та його застосування для перевірки номінального ВВП України на шахрайство та маніпуляції.
Щодня працюючи з українською макроекономічною статистикою, аналітики спостерігають постійні перегляди історичних даних (іноді досить значні) або несподівано значні стрибки та падіння, які важно пояснити (серед нещодавніх прикладів – несподівано різке зростання ВВП у 4 кварталі 2016 року – з +2,3% у 3 кварталі до +4,8% відносно відповідних кварталів попереднього року). Тож не дивно, що експерти часто не довіряють статистиці. Проте в нас немає інших варіантів, окрім використання наявних даних.
Усі розуміють важливість ВВП як основного показника стану економіки. Окрім того, ВВП – це невід’ємна складова інших економічних показників, таких як ВВП на душу населення, баланс державного бюджету (% ВВП) та державний борг (% ВВП), якими користуються політики, міжнародні фінансові організації та іноземні інвестори для порівняння різних країн. Отже, не дивно, що існує спокуса маніпулювати статистикою ВВП, особливо враховуючи, що методологія розрахунку цього показника є дуже складною, і мало хто може назвати себе експертом у цій галузі. У цій статті ми розглянемо один із можливих методів перевірки макроекономічних даних на маніпуляції та шахрайство, який успішно застосовують аудитори, працюючи з даними бухгалтерського обліку. Цей метод ґрунтується на Законі Бенфорда.
У 2011 році Раух, Гьоттше, Брелєр та Енгель опублікували досить відому статтю «Факти та вигадки урядових економічних даних ЄС», у якій проаналізували макроекономічні дані держав Європейського Союзу (ЄС) за допомогою закону (феномену) першої цифри чи Закону Бенфорда. Вони виявили, що серед країн Євросоюзу, дані Греції найсильніше відхиляються від розподілу Бенфорда. Такий висновок вказує на аномалію в грецькій статистиці, що узгоджується зі скандалом про маніпулювання статистичними даними – якщо коротко, щоб відповідати вимогам ЄС Греція фальсифікувала свою статистику. Таким чином закон першої цифри виявився хорошою перевіркою доброчесності не лише облікових даних, але й макроекономічної статистики. У цій статті ми застосовуємо це відкриття і досліджуємо номінальний ВВП України стосовно підозрілих відхилень.
Про Закон Бенфорда
Тож що таке Закон Бенфорда і як він працює? Закон Бенфорда стверджує, що «в багатьох наборах чисел, що зустрічаються в природі, перша значуща цифра, ймовірно, буде невеликою». Вперше цей закон був відкритий знаменитим астрономом Саймоном Ньюкомом (1881), але, як це часто трапляється, відкриття не набуло популярності й поступово забулося. Півстоліття потому інженер Френк Бенфорд (1938) повторно «віднайшов» це явище і навіть вдало протестував його на 20 різних наборах даних (фізичні константи, площі басейнів річок, адреси вулиць, тощо), і тепер це явище названо на його честь.
Можливо, розумінню явища першої цифри сприятиме знайомство з історією його відкриття. Як Ньюком, так і Бенфорд помітили, що перші сторінки логарифмічних таблиць, що починаються з одиниці, потріпані сильніше ніж інші сторінки, що свідчить про те, що цифра 1 зустрічається «у природі» набагато частіше. Логарифмічна шкала (Рисунок 1) добре ілюструє чому так трапляється.
Рис. 1. Логарифмічна шкала

Наприклад, візьмемо відрізок від 1 до 10. Випадково обране число x починається з цифри 1, якщо 1≤x<2 або log 1≤log x<log 2. Число x починається з цифри 2, якщо 2≤x<3 або log 2≤log x<log 3. І так далі. Як бачимо, інтервал [log 1 = 0, log 2 = 0,30) ширший за інтервал [log 2 = 0,30, log 3 = 0,48), і якщо продовжити, інтервал дедалі зменшуватиметься. Приблизно 30% обраного діапазону займає перший інтервал. Ці розрахунки справедливі для діапазонів від 10 до 100, від 100 до 1000 тощо.
При цьому, згідно з цим законом, значущі цифри підлягають наступному логарифмічному розподілу:
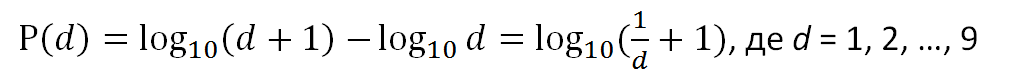
що графічно представлено на Рисунку 2.
Рис. 2. Розподіл перших цифр згідно з Законом Бенфорда
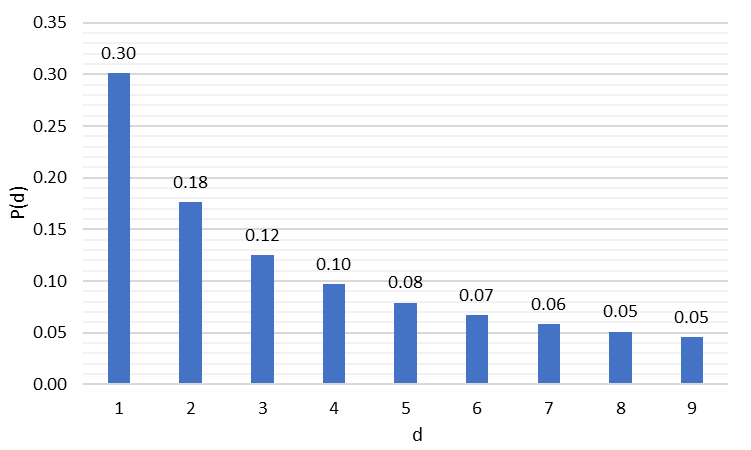
Як бачимо, відповідно до Закону, у масивах даних цифра 1 зустрічається як перша цифра у 30% випадків, тоді як частота появи цифр від 2 до 9 поступово знижується. У Таблиці 1 наведено емпіричні результати Бенфорда, що показують, наскільки вони наближені до теорії.
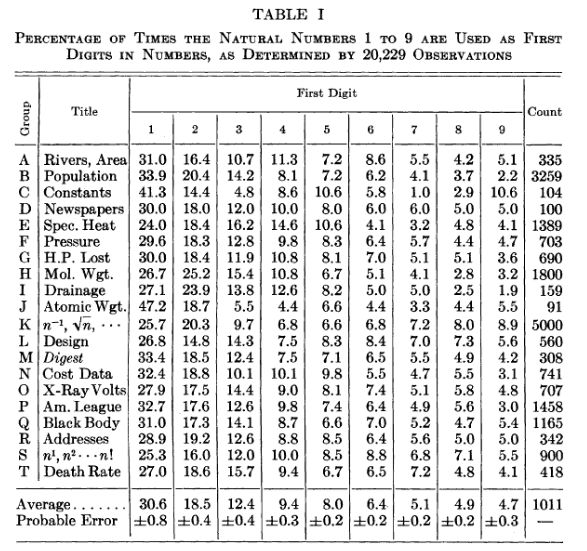
Джерело: Бенфорд «Закон аномальних чисел» (1938)
Дані ВВП України
Тепер ми можемо перевірити статистику ВВП України. Ми взяли номінальний ВВП із квартальною періодичністю за період з 1 кварталу 2001 року до 1 кварталу 2014 року. Ми розглядаємо 1 квартал 2001 року як відправну точку, оскільки це найбільш ранній звітний період, представлений на сайті Укрстату. Наприкінці 2013 року та на початку 2014 року Україна зазнала значних соціально-геополітичних потрясінь, унаслідок чого після 1 кварталу 2014 року офіційна статистика представлена без урахування Криму та частини Донбасу. Тому ми не розглядаємо період після 1 кварталу 2014 року; у цьому випадку ми зберігаємо узгодженість даних. З метою збільшення кількості одиниць спостережень ми також включили до нашого аналізу основні компоненти ВВП (зі сторони видатків), такі як споживання домогосподарств, державні видатки, інвестиції, експорт та імпорт.
Частота появи першої значущої цифри номінального ВВП України подано на Рисунку 3.
Рис. 3. Номінальний ВВП України: частотний розподіл першої цифри
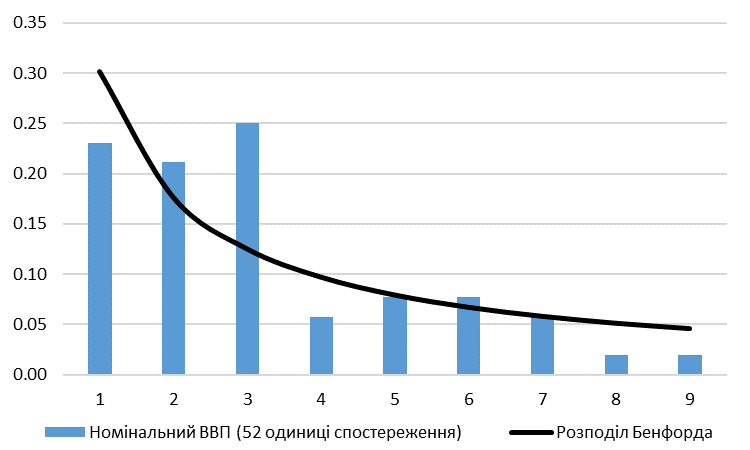
Частотний розподіл першої цифри номінального ВВП досить сильно відрізняється від розподілу Бенфорда. Однак причиною цього може бути невелика вибірка (52 одиниці спостереження). Використання компонентів ВВП вирішує проблему малої вибірки (Рисунок 4).
Рис. 4. Компоненти номінального ВВП України: частотний розподіл першої цифри
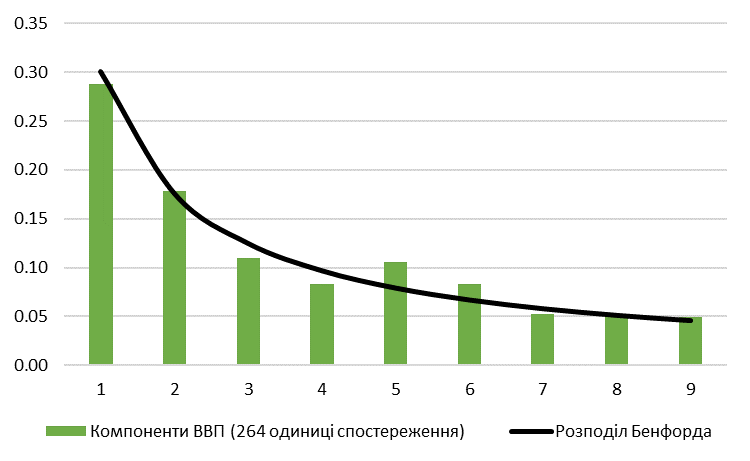
Використавши компоненти номінального ВВП, ми змогли розширити нашу вибірку до 264 одиниць спостереження. Схоже, що статистика номінального ВВП України відповідає закону першої цифри. Проте для нашого аналізу також важливо подивитися як віглядають українські данні на тлі інших. Тож ми беремо статистику ВВП для низки країн та обчислюємо відхилення від розподілу Бенфорда, застосовуючи формулу хі-квадрату:
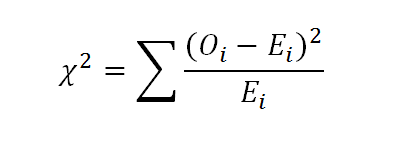
де Oi – це спостережуване значення, а Ei – це очікуване значення (розподіл Бенфорда).
З огляду на те, що розподіл Бенфорда інваріантний за зміни масштабу (Пінкхам 1961), ми можемо порівнювати різні країни, навіть якщо їхній номінальний ВВП розрахований у різних валютах. Усі дані зібрано на офіційних веб-сайтах відповідних державних служб статистики. Порівняльна статистика X2 (хі-квадрату) подана на Рисунку 5.
Рис. 5. Порівняльна статистика критерію хі-квадрату
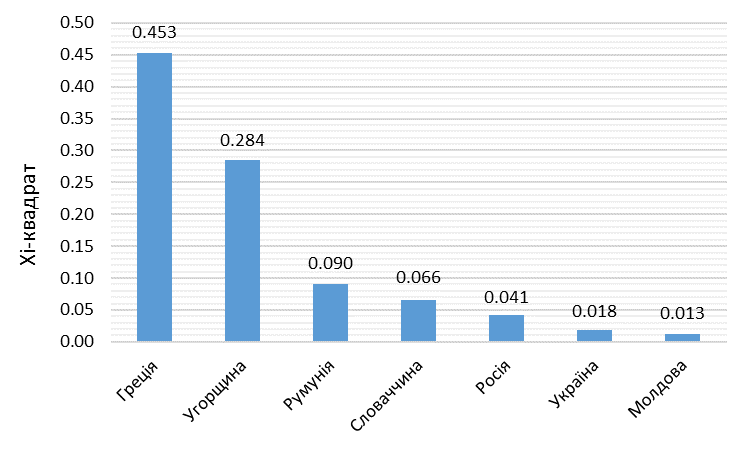
У даних Греції спостерігається найбільше відхилення від розподілу Бенфорда, тоді як Україна має один з найнижчих X2 серед аналізованих країн.
Висновки
Закон Бенфорда зарекомендував себе як якісний інструмент для виявлення маніпуляцій з даними бухгалтерського обліку. Нещодавні дослідження вказують на те, що його також можна застосовувати й до макроекономічних даних. У цьому дослідженні ми показуємо, що компоненти номінального ВВП України мають одне з найменших відхилень від розподілу Бенфорда серед семи країн, які ми включили до нашого аналізу (Греція, Угорщина, Румунія, Словаччина, Росія, Україна та Молдова). Водночас статистика Греції найбільше відхиляється від теоретичних показників, що підтверджує факт маніпулювання даними, виявлений Європейською комісією.
Таким чином, номінальний ВВП України успішно пройшов перевірку законом першої цифри, що вказує на те, що дані не зазнали зовнішнього впливу чи маніпуляції (принаймні, ґрунтуючись на описаному вище тесті).
Посилання:
Benford, F. (1938), ‘The Law of Anomalous Numbers’, Proceedings of the American Philosophical Society 78, 551–572.
Benford, F. (1938), ‘The Law of Anomalous Numbers’, Proceedings of the American Philosophical Society 78, 551–572.
Benford, F. (1938), ‘The Law of Anomalous Numbers’, Proceedings of the American Philosophical Society 78, 551–572.
Benford, F. (1938), ‘The Law of Anomalous Numbers’, Proceedings of the American Philosophical Society 78, 551–572.
Berger, A., T. P. Hill (2011), ‘Benford’s Law Strikes Back: No Simple Explanation in Sight for Mathematical Gem’, The Mathematical Intelligencer 33(1).
European Commission (2010), ‘Report on Greek Government Deficit and Debt Statistics’.
Newcomb, S. (1881), ‘Note on the Frequency of Use of the Different Digits in Natural Numbers’, American Journal of Mathematics 4, 39–40.
Pinkham, R. S. (1961), ‘On the Distribution of First Significant Digits’, Annals of Mathematical Statistics 32, 1223–1230.
Rauch, B., M. Göttsche, M. Brähler and S. Engel (2011), ‘Fact and Fiction in EU-Governmental Economic Data’, German Economic Review 12(3), 243-255.
Головне фото: depositphotos.com / bakhtiarzein
Застереження
Автор не є співробітником, не консультує, не володіє акціями та не отримує фінансування від жодної компанії чи організації, яка б мала користь від цієї статті, а також жодним чином з ними не пов’язаний



