ВВП Украины: Проверка на предмет манипуляций

В статье кратко рассмотрен Закон Бенфорда и его применение для проверки номинального ВВП Украины на предмет мошенничества и манипуляций.

Ежедневно работая с украинской макроэкономической статистикой, аналитики наблюдают постоянные пересмотры исторических данных (иногда весьма значительные) или неожиданно большие скачки и падения которые трудно объяснить (среди недавних примеров – удивительно резкий рост ВВП в 4 квартале 2016 года – с +2,3% в 3 квартале до +4,8% по сравнению с соответствующими кварталами предыдущего года). Неудивительно, что эксперты зачастую не доверяют статистике. Однако у нас нет иного выбора, кроме как пользоваться имеющимися данными.

Каждый понимает важность ВВП как основного показателя состояния экономики. Кроме того, ВВП – это неотъемлемая составляющая других экономических показателей, таких как ВВП на душу населения, баланс государственного бюджета (% ВВП) и государственный долг (% ВВП), которыми пользуются политики, международные финансовые организации и иностранные инвесторы для сравнения разных стран. Поэтому не удивительно, что существует соблазн манипулировать статистикой ВВП, особенно учитывая, что методология расчета этого показателя является очень сложной, и мало кто может назвать себя экспертом в этой области. В этой статье мы рассмотрим один из возможных методов проверки макроэкономических данных на предмет манипуляций и мошенничества, который успешно применяется аудиторами, при работе с данными бухгалтерского учета. В основе этого метода лежит Закон Бенфорда.

В 2011 году Раух, Гёттше, Брэлер и Энгель опубликовали довольно известную статью «Факты и вымыслы правительственных экономических данных ЕС», в которой проанализировали макроэкономические данные государств Европейского Союза (ЕС) с помощью закона (феномена) первой цифры или Закона Бенфорда. Они обнаружили, что среди стран Евросоюза, данные Греции сильнее всего отклоняются от распределения Бенфорда. Такой вывод указывает на аномалию в греческой статистике, что увязывается со скандалом о манипуляции статистическими данными – в двух словах, чтобы соответствовать требованиям ЕС Греция фальсифицировала свою статистику. Таким образом закон первой цифры оказался хорошей проверкой добросовестности не только данных учета, но и макроэкономической статистики. В данной статье мы применяем это открытие и исследуем номинальный ВВП Украины на предмет подозрительных отклонений.

О Законе Бенфорда

И все же что такое Закон Бенфорда и как он работает? Закон Бенфорда гласит, что «во многих встречающихся в природе наборах чисел первая значащая цифра, вероятно, будет небольшой». Впервые этот закон был открыт знаменитым астрономом Саймоном Ньюкомом (1881), но, как это часто случается, открытие не приобрело популярности в свое время и постепенно забылось. Полвека спустя инженер Фрэнк Бенфорд (1938) повторно «обнаружил» это явление и даже успешно протестировал его на 20 различных наборах данных (физические константы, площади бассейнов рек, адреса улиц и т.д.), и теперь это явление носит его имя.

Возможно, пониманию явления первой цифры поспособствует знакомство с историей его открытия. Как Ньюком, так и Бенфорд обнаружили, что первые страницы логарифмических таблиц, начинающиеся с единицы, потрепаны сильнее, чем остальные страницы, что свидетельствует о том, что цифра 1 встречается «в природе» гораздо чаще. Логарифмическая шкала (Рисунок 1) хорошо иллюстрирует почему так происходит.

К примеру, возьмем диапазон от 1 до 10. Случайно выбранное число начинается с цифры 1, если 1≤x<2 или log 1≤log x<log 2. Число x начинается с цифры 2, если 2≤x<3 или log 2≤log x<log 3. И так далее. Как видим, интервал [log 1 = 0, log 2 = 0,30) шире чем [log 2 = 0,30, log 3 = 0,48), и если продолжить, интервал будет постепенно сокращаться. Примерно 30% выбранного диапазона занимает первый интервал. Эти расчёты справедливы для диапазонов от 10 до 100, от 100 до 1000 и т.д.

При этом, согласно этому закону, значимые цифры подлежат последующему логарифмическому распределению:

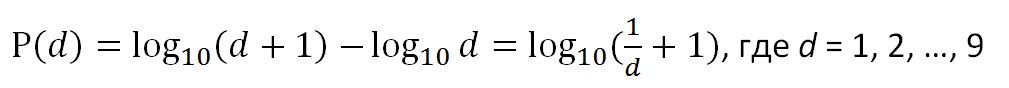
что графически представлено на Рисунке 2.

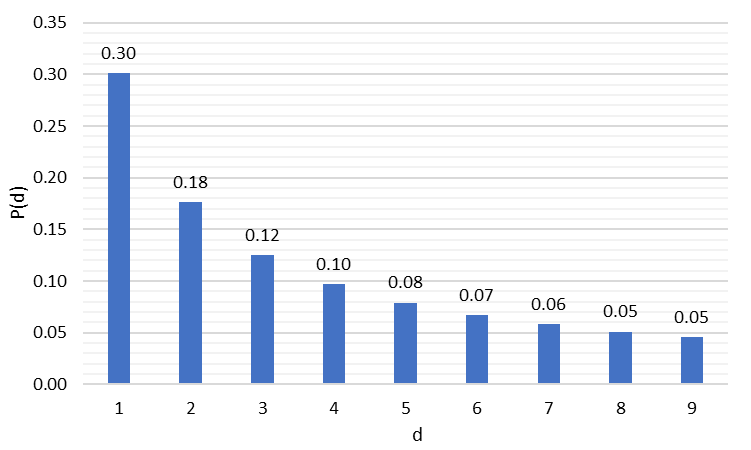
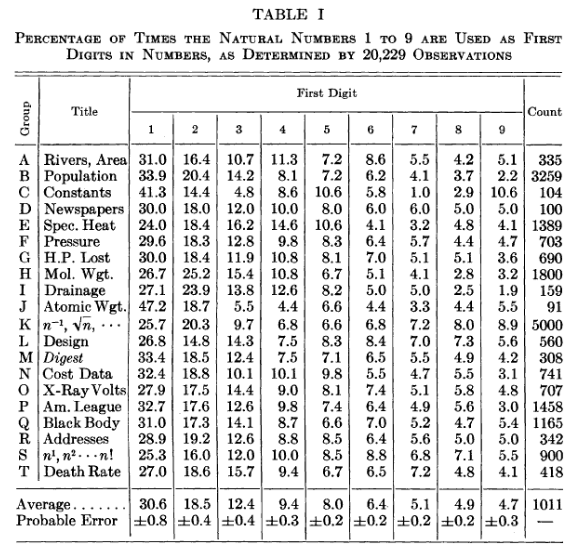
Как видим, согласно Закону, в массивах данных цифра 1 встречается как первая цифра в 30% случаев, в то время как частота появления цифр от 2 до 9 постепенно снижается. В Таблице 1 приведены эмпирические результаты Бенфорда, показывающие, насколько они приближены к теории.

Данные ВВП Украины

Теперь мы можем проверить статистику ВВП Украины. Мы взяли номинальный ВВП с квартальной периодичностью за период с 1 квартала 2001 года по 1 квартал 2014 года. В качестве отправной точки мы рассматриваем 1 квартал 2001 года, поскольку это самый ранний отчетный период, представленный на сайте Укрстата. В конце 2013 года и в начале 2014 года Украина пережила значительные социально-геополитические потрясения, в результате чего после 1 квартала 2014 года официальная статистика предоставлена без учета Крыма и части Донбасса. Поэтому мы не рассматриваем период после 1 квартала 2014 года; в этом случае мы сохраняем согласованность данных. С целью увеличения количества единиц наблюдений мы также включили в наш анализ основные компоненты ВВП (со стороны расходов), такие как потребление домохозяйств, государственные расходы, инвестиции, экспорт и импорт.

Частота появления первой значимой цифры номинального ВВП Украины представлена на Рисунке 3.

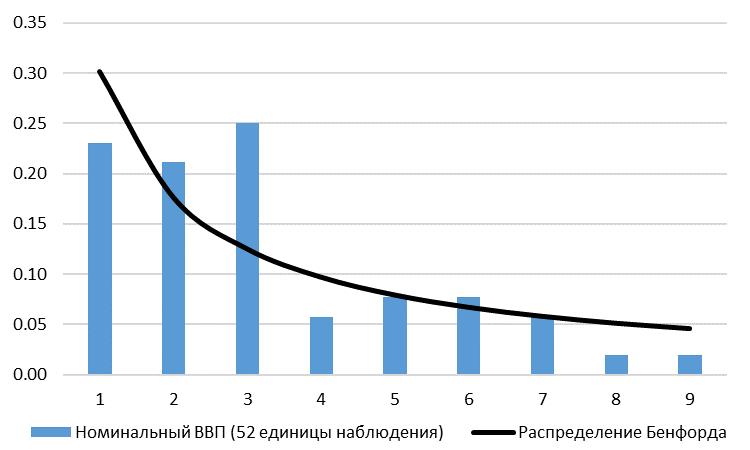
Частотное распределение первой цифры номинального ВВП достаточно сильно отличается от распределения Бенфорда. Однако причиной этому может быть небольшая выборка (52 единицы наблюдения). Использование компонентов ВВП решает проблему малой выборки (Рисунок 4).

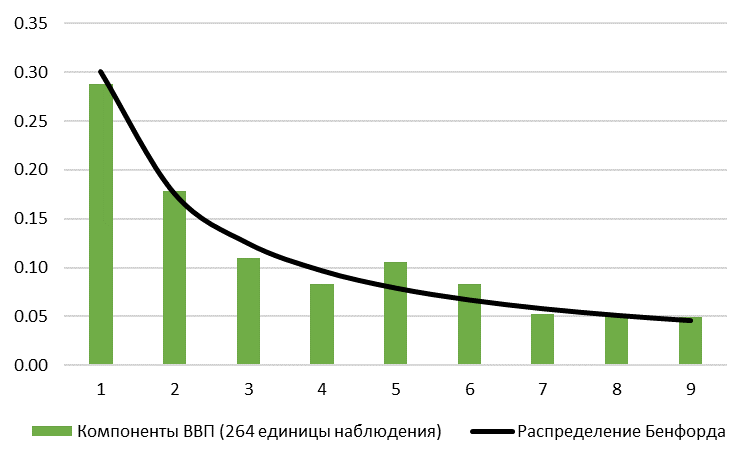
Использовав компоненты номинального ВВП, мы смогли расширить нашу выборку до 264 единиц наблюдения. Похоже, что статистика номинального ВВП Украины соответствует закону первой цифры. Однако для нашего анализа также важно посмотреть как выглядят украинские данные на фоне других. Поэтому мы берем статистику ВВП для ряда стран и вычисляем отклонение от распределения Бенфорда по формуле хи-квадрата:

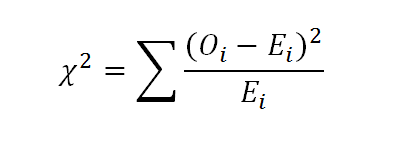
где O_i – это наблюдаемое значение, а E_i – это ожидаемое значение (распределение Бенфорда).

Учитывая то, что распределение Бенфорда инвариантно при изменении масштаба (Пинкхам 1961), мы можем сравнивать разные страны, даже если их номинальный ВВП рассчитан в разных валютах. Все данные были собраны на официальных сайтах соответствующих государственных служб статистики. Сравнительная статистика Х² (хи-квадрата)  представлена на Рисунке 5.

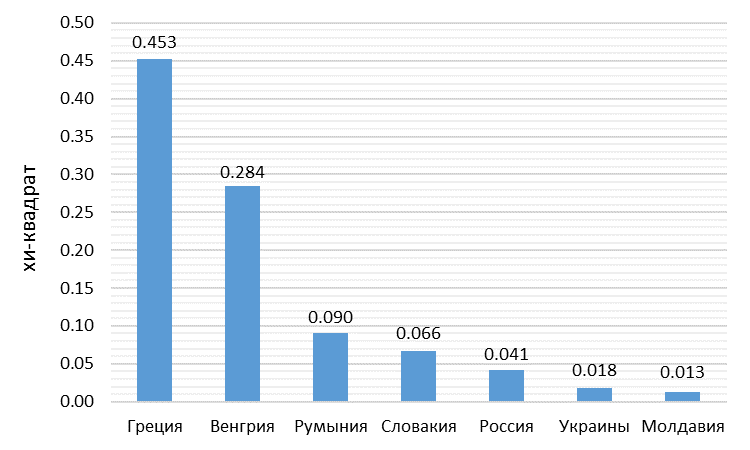
В данных Греции наблюдается наибольшее отклонение от распределения Бенфорда, в то время как у Украины один и самых низких Х² среди проанализированных стран.

Выводы

Закон Бенфорда зарекомендовал себя как качественный инструмент для выявления манипуляций в данных бухгалтерского учета. Последние исследования указывают на то, что его также можно применять и к макроэкономическим данным. В этом исследовании мы показываем, что компоненты номинального ВВП Украины имеют одно из самых малых отклонений от распределения Бенфорда среди семи стран, которые мы включили в наш анализа (Греция, Венгрия, Румыния, Словакия, Россия, Украина и Молдова). В то же время статистика Греции больше всех отклоняется от теоретических показателей, что подтверждает факт манипуляции данными, обнаруженный Европейской комиссией.

Таким образом, номинальный ВВП Украины успешно прошел проверку законом первой цифры, что указывает на то, что данные не подвергались постороннему вмешательству или манипуляциям (по крайней мере, основываясь на описанном выше тесте).

Ссылки